PCR/qPCR 数据分析
PCR/qPCR 定性数据分析
传统 PCR 完成后,数据通过琼脂糖凝胶或最近的毛细管电泳系统进行解析分析。在某些应用中,qPCR 将与用于分析的终点数据一起运行,例如用于 SNP 基因分型。在每种情况下,终点数据都能在 PCR 达到平稳期后提供定性分析。在某些情况下,可以通过分析终点数据对 PCR 产率进行半定量分析,但定量测量更常用 qPCR 和定量周期值(Cq)1 值分析。
qPCR 数据分析
在本指南中,强调了导致使用 PCR 或 qPCR 测量核酸时出现差异的因素。这些因素中的每一个都应进行优化,以便使检测结果尽可能接近反应中基因(目标)的实际数量。这些过程的结果是为每个样本中的每个目标生成一组 Cq 值。本章将介绍推导和分析这些 Cq 值的过程,以提供代表生物学故事的可靠数据。
得出准确的 Cq Values
基线校正
为每个样本中的每个目标确定一个 Cq 值。与不同仪器相关联的不同分析软件包有不同的方法来确定 Cq (也使用不同的名称,例如 Ct、Cp、起飞点)。深入探讨所有这些算法的细节超出了本指南的范围。不过,基于扩增曲线的 qPCR 测量对背景荧光很敏感。背景荧光可能是由一系列因素造成的,其中包括塑料容器的选择、未淬灭的剩余探针荧光、漏入样品孔的光线以及特定微孔板孔的光学检测差异。在设计良好的检测中,本底信号与放大信号相比是很低的。然而,背景信号的变化可能会妨碍不同样品的定量比较。因此,必须校正导致基线差异的本底荧光变化(图 10.1)。
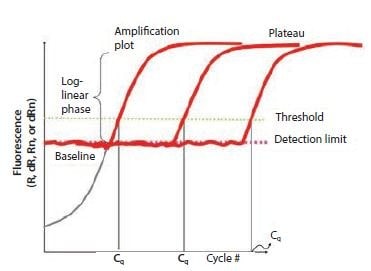
图 10.1扩增图的组成部分。该图显示了不同样品的荧光随循环次数的增加而增加。阈值设置在检测限之上,但远远低于扩增速度减慢的高原阶段。
一种常见的方法是使用早期周期(如周期 5 至 15)中的荧光强度来确定背景荧光中恒定的线性成分。然后将其定义为扩增图的背景或基线。由于瞬时效应,建议避免在最初几个周期(如周期 1 至 5)进行基线定义,因为这些周期通常会出现反应稳定伪影。用于基线校正的周期越多,基线变化的线性分量的潜在准确性就越高。许多仪器软件包允许手动设置用于基线定义的周期。
基线设置的效果示例见图 10.1。可以看出,Cq 值和放大图的明显形状会受到准确基线设置的影响。在示例中,标有 C3 的曲线的基线被错误地手动调整,因此基线周期是从周期 5 到周期 31 的数据计算出来的。这导致曲线跌落到零基线水平(图 10.2A),Cq 为 28.80。为了纠正这种情况,需要查看原始数据 R,并确定线性背景的最后一个周期(扩增前的最后一个周期)。在 图 10.2B中,可以看到这是周期 22。基线被正确设置为周期 5 和周期 22 之间的零值(图 10.2C),然后对扩增图进行校正 (图 10.2D)。修正后的 Cq 为 26.12。因此,请注意,在基线设置不正确和正确的情况下,Cq 值之间存在很大差异,这表明设置正确的基线是数据分析的重要组成部分。
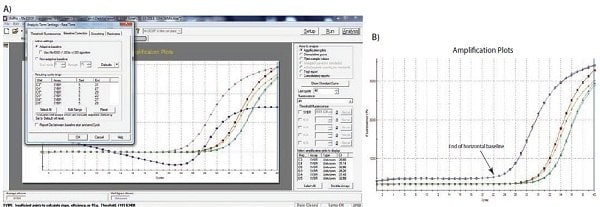
图 10.2A-B.A)基线设置不正确时,数据低于归一化荧光读数零值的典型示例(蓝色扩增图)。B) 相同扩增图的原始数据显示了线性基线的极限,数据没有出错。

图 10.2C-D.C)基线的起点和终点界限可通过相应的软件设置来定义。D)应用校正基线设置可获得高质量的数据
设置阈值
虽然有些研究人员主张绘制单个扩增图来估计测量样本中的扩增效率和目标量2,3,4,但最原始、最常用的方法是使用阈值来推导 Cq&bsp;2,3,4,但推导 Cq 最原始、最常见的方法是使用阈值。
阈值法背后的原理是:为了使 qPCR 扩增产生的相关荧光信号可视化,信号必须增加,使其高于仪器的检测限(因此也高于基线;图 10.1)。为此所需的循环次数与样本中目标物的初始拷贝数成正比。因此,如果原始拷贝数较低,则需要更多的循环才能使信号增加到基线以上;如果拷贝数较高,则需要更少的循环。由于基线设定在系统的检测极限,因此在基线上进行的测量会非常不准确。
阈值强度的选择需要遵守一些基本原则。对于给定的目标和所有要比较的样本,阈值必须设置为固定的强度。如果样品数量太多,单个平板无法容纳,则必须采用平板间校准方案,例如加入作为平板间对照的重复对照或标准曲线序列稀释。理论上,阈值可以设置在扩增曲线对数线性阶段的任何位置。然而,在实际操作中,扩增的对数线性阶段可能会受到背景荧光基线漂移、高原阶段或检测效率差异的干扰,因此在较高的循环中会出现扩增图梯度。建议阈值设置如下:
- 足够高于背景荧光基线,以确保避免扩增图因背景荧光而过早越过阈值。
- 在扩增图的对数阶段,不受高原阶段的影响(通过对数视图查看扩增图最容易发现这一点, 图 10.3A)。
- 在所有放大图的对数相位平行的位置。
阈值设置过程在 图 10.3 中演示。在 图 10.3A 中,放大图以 Y 轴对数刻度显示,从而提供了放大对数相位的可视化扩展,并将其显示为放大图的线性部分。阈值设置在该对数相位内的最高荧光强度处(参考 Y 轴),在该处所有扩增图都是平行的。然后将刻度返回线性视图(图 10.3B),显示符合阈值设置要求的最高设置。或者,也可以将阈值设置在该对数相位的下端(图 10.3C and 10.3D)。只要扩增图的对数相位是平行的,样品间的ΔCq 就不受阈值设置的影响。
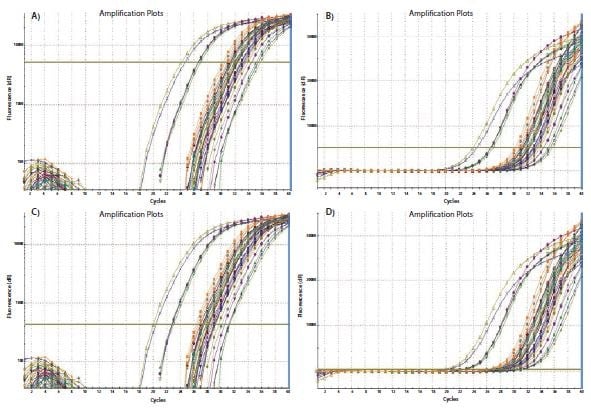
图 10.3阈值设置会影响记录的绝对 Cq 值,并可能影响样本之间的 ΔCq。A).使用数据的对数与线性图,将阈值设置在荧光强度最高但扩增图显示平行对数相位的位置。B).保持 A) 中的阈值设置,并显示在线性对线性图上。C).使用数据的对数与线性图,将阈值设置在荧光强度最低但扩增图显示平行对数相位的位置。D).阈值设置与 C) 保持一致,并显示在线性对线性图上。在每种情况下,样品之间的 ΔCq 值都是相同的。
当在分析中包含较高周期的数据时,在扩增图的对数线性相位平行的位置设置阈值的要求变得更加相关。在较高 Cq 的数据集上重复了针对 图 10.3 中的数据所描述的阈值设置过程,结果见 图 10.4。得出的 Cq data in Table 10.1 中的数据说明了 Cq 的变化,更重要的是说明了具有三个阈值设置的三个扩增图的 ΔCq 值(图 10.4)。由于扩增图不平行,ΔCq 值以及每个样品中目标物相对数量的估计值高度依赖于阈值的设置(图 10.4)。
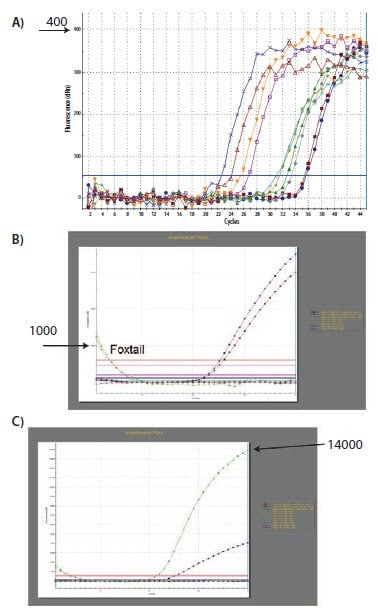
图 10.4.使用不同的数据集重复图 10.3 中的分析。在这种情况下,由于高 Cq 时反应效率的不同,扩增图并不平行。A) 和 B) 的最低设置与 C) 和 D) 的最高设置所产生的 ΔCq 值不同(见表 10.1)。
qPCR 定量策略
准确的基线和阈值设置对可靠的定量至关重要。在设置了每个基线和阈值后,就会生成一个 Cq 值,并以此为基础进行定量。
标准曲线定量
顾名思义,标准曲线定量需要使用标准曲线来确定测试样品中的目标物数量。因此,样品的所有测定量都是相对于标准曲线的测定量而言的。这就要求在进行每组样品反应的同时,运行额外的外部标准。标准曲线材料的选择对于消除因样品和标准物质的检测效率不同而导致的潜在定量差异非常重要。外部标准物质的引物结合位点必须与目标物中的引物结合位点相同,包含与目标物相同的序列,具有相似的复杂性,并以尽可能相似的方式处理。因此,在测量 cDNA 中目标物的浓度时,最好在对照样本的序列稀释液中测量相同的 cDNA。然而,有些研究由于实际原因无法做到这一点,因此必须尽可能接近地再现样本条件,例如,在人工寡核苷酸标准或携带标准序列的线性化质粒中加入与测试物种无关的物种的 gDNA。一旦确定了合适的构建体或扩增子,就可以生成序列稀释的标准曲线。测定每个标准品的目标 Cq ,并以对数标度绘制其与浓度或相对浓度/稀释因子的对比图。这样就形成了一条标准曲线,然后通过比较未知样品扩增得出的 Cq 值来确定测试样品的浓度。使用标准曲线进行定量时,阈值设置必须保持不变,以确定同一平板上标准品和样品的 Cq 。不同平板的阈值可能不同。
相对/比较定量
相对或比较定量使用 Cq 的差异作为不同样品中目标序列浓度差异的决定因素。这种方法不像标准曲线法那样测量每个样品中的目标物数量,而是得出一组数据,显示不同样品之间的倍数变化。
在这种方法的最初形式5中,所有检测的效率都被假定为 100%,从而导致假定 Cq&csub>q 差值为 1(ΔCq = 1)是目标物相差 2 倍的结果。要确定目的基因或相关基因(GOI)的折叠变化,数据还必须参照负载对照(参考基因,ref;有关数据归一化的讨论见下文)。
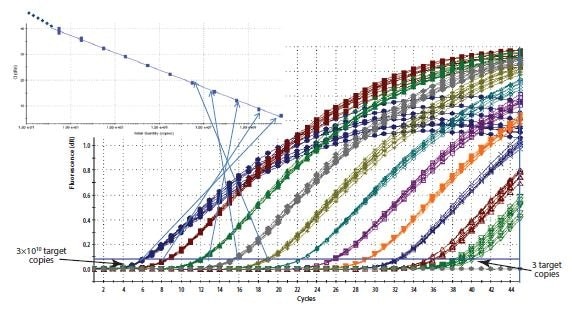
图 10.5.构建标准曲线。将稀释系列中每个样品记录的 Cq 与相对浓度的对数线性比例绘制成曲线。
在 式 1中,两个样本(A 相对于 B)的 GOI 比值在校正为参考基因后的测量值为:2(假设反应效率为 100%)除以 2,再加上 GOI 的 Cq 值的幂:2(假定反应效率为 100%)除以 GOI 的 Cq 值差异的 2(假定反应效率为 100%),再除以参考基因的 Cq 值差异的 2(假定反应效率为 100%),再除以参考基因的 Cq 值差异的 2
。
公式 1.原始(利瓦克)相对量化模型。
然而,正如分析优化和验证中所述,反应的效率差异很大,这会对数据产生很大影响。因此,对公式 1中的假设进行了处理(公式 2)6,以便将反应效率的差异纳入分析。在这种情况下,扩增因子 2 被 PCR 的实际效率所取代(由标准曲线分析确定;见 Assay Optimization and Validation)。

公式 2.效率调整(Pfaffl)相对量化模型
表 10.2 中列出了一组 Cq 值,作为使用效率调整(公式 2)相对定量模型的示例。GOI 的效率为 1.8,参考基因的效率为 1.94。
这是一个非常简单的研究示例,要求测量两个样本中一个基因与单一参考基因归一化后的折合差。该比值显示了样本 2 中 GOI 相对于样本 1 的折叠变化,该变化是根据单一参考基因校正后得出的。然而,选择一个合适的参考基因往往是不可能的,因此,人们提出了更复杂的归一化方法。
归一化
大多数基于 PCR 的实验的主要目的是解决样本中是否存在目标基因(未知,UNK)这一基本问题。最简单的方法是检测凝胶,检查片段中是否存在所需的 GOI。当片段存在时,对片段大小的确认可确保检测结果呈阳性。但是,如果不存在,则有可能出现假阴性结果。因此,关键是要重复检测试验,并进行至少一次额外的 PCR,作为负载和阳性 PCR 对照。通用抑制对照检测 SPUD(见样品纯化和质量评估)可用于支持对阴性结果的信心。另一种方法是对参考基因进行特异性检测。传统上,检测参考基因、GAPDH、18S 核糖体 RNA 或 β 肌动蛋白的 PCR 检测与检测 GOI 的 PCR 检测同时进行,并在凝胶上显现所产生的片段。GAPDH、18S 核糖体 RNA 和 β 肌动蛋白是组成型表达的,因此在半定量分析中被用作负载对照。然而,很快我们就发现,无论实验设计如何,这些基因并不是在所有细胞中都以相同的浓度普遍表达。因此,在测量相对核酸浓度(通常是 cDNA,但也包括 gDNA)时,就需要一个稳定的参照物,例如,在检测基因的拷贝数变异时。
归一化是将技术测量结果修正为稳定参照物的过程,以便检测真实的生物变异。对技术差异进行归一化处理的方法有很多,这意味着必须选择并验证适合特定实验的方法7。必须认识到,采用不恰当的归一化技术可能比不归一化更不利于整个分析过程8。
样本质量对检测归一化的影响
样本的完整性和纯度对 qPCR 和 RT-qPCR 目标量测定的影响已被详细讨论(
Sample Purification and Quality Assessment,样品质量控制和 Reverse Transcription,反转录)。研究表明,样品中的抑制剂和 RNA 降解对特定目标9的测量有不同的影响。抑制剂对任何靶标的测量都有影响,但程度不同,取决于检测设计。总 RNA 降解会影响 mRNA 和 miRNA 的测量10,这同样高度依赖于整体实验设计。因此,关键是要考虑模板浓度对 RT 反应的影响,以及归一化后样本质量对数据的影响。归一化不能抵消低质量检测或样本的影响(请参阅Assay Optimization and Validation)。
归一化方法
实际上,归一化方法可以抵消在进行 qPCR 分析所需的多步骤过程中可能引入的变异性(图 10.6)。然而,在流程中的任何一个阶段应用归一化方法,都可能无法控制在较早或较晚阶段已经或将要出现的技术误差和/或偏差。归一化方法并不是相互排斥的,因此建议采用组合控制11。
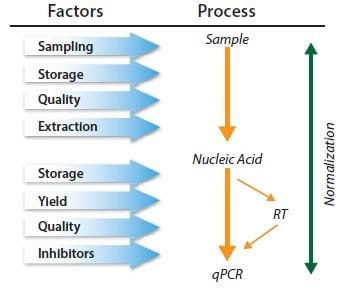
图 10.6.qPCR 是一个多步骤的过程,必须对每个步骤进行控制。必须在一系列对照中考虑归一化。
归一化的目的是提供一个稳定的参考点,以便测量结果可以参照;因此,选择的归一化因子必须是在整个实验过程中稳定的测量结果。这可以是稳定的参考基因,也可以是细胞数、组织质量、RNA/DNA 浓度、外部峰值12或全局表达基因的代表性测量值等替代指标之一。
参考基因选择
参考基因是其数量不会因实验而改变的目标基因。在对 DNA 拷贝数变异进行量化时,相关序列的拷贝数可能会发生变化,这时只需以已知不会发生变化的替代基因组区域为目标,对测量结果进行归一化处理即可。在测量人类表皮生长因子受体 2 (HER-2) 基因组扩增13时,就是一个应用这种方法的例子。HER-2基因组不稳定性是乳腺癌的一个预后指标,准确测量HER-2扩增状态对患者管理非常重要。
在测量基因表达时,参考基因是指 mRNA 浓度不会因实验而改变的靶标。举例来说,在细胞单层中加入一种有丝分裂化合物后,将测量对基因 X 表达的影响。因此,还需要测量另一个(或多个)已知不受有丝分裂原影响的基因。这就给研究人员提出了一个直接挑战,即在能够研究 GOI 之前,找到一个不受实验程序影响的 mRNA 靶点。这种验证参考基因的过程是准确测量 GOI 的基础。最广泛使用的归一化方法是忽略这一过程,将基因表达数据归一化为单一的、未经验证的参考基因。这种做法并不可取,而且直接违背了 MIQE 准则1。RT-qPCR 的 mRNA 定量通常会因参考基因选择不当而受到影响。不能因为引物已在冰箱中、历史上曾在 Northern 印迹中使用过、同事使用过或其他实验室在不同实验中使用过,就按照相对常见的做法使用参考基因。参考基因需要在特定的实验情况下进行验证,以确保相关参考基因不受实验影响。如果没有进行验证,而参考基因受到了实验的影响,那么结果可能是不正确的,随后的解释很可能导致毫无意义的数据8。
有一系列科学文献介绍了不同的归一化方法7-14 还有大量出版物介绍了为特定实验方案确定最合适的归一化基因所需的规程。
选择稳定的参考基因要求分析师在代表测试和对照 mRNA 的样本子集上评估 qPCR 对一些(通常 10 到 20 个基因)候选 mRNA 靶标7 的稳定性。完整的方案见 15、GeNorm14、Bestkeeper16 或 NormFinder17 等程序的不同分析方法结合使用。
参考基因稳定性分析
参考基因实际上是 qPCR 相对定量测定的支点。因此,参比基因的稳定性对整个检测的可靠性至关重要。如果参比基因的表达在不同样品之间发生变化,这种变化将直接转移到定量结果中,增加的变异性可能会掩盖预期的可观察到的生物效应,更有甚者,可能会造成完全人为的生物效应表象,与实际的相关基因无关。
可以说,最重要的安全措施是不仅使用一个参考基因,而且使用两个或更多参考基因。可以对多个参考基因的表达进行平均,以减少归一化带来的技术变异。这有助于提高微小生物效应测量的显著性。然而,更重要的是,两个或多个参考基因可以相互控制,以保持稳定性,并控制可能影响其中一个参考基因表达水平的意外情况。
另一项安全措施是使用一种以上的方法来鉴定稳定的参考基因。
表 10.3 列出了我们之前与 EMBL 共同举办的研讨会上评估过的候选参考基因列表。样本采集自两个不同处理组的人类细胞培养物。
NormFinder和geNorm算法的开发都基于这样一个假设:测试大量候选参考基因可用于对单个候选参考基因的稳定性进行排序。举例来说,如果所有候选参考基因都围绕稳定表达水平随机变化,那么这一假设可能是正确的。然而,现实情况未必如此。因此,为避免误导结果,谨慎的做法是避免使用受调控的候选参考基因,尤其是共调控的候选参考基因。
表 10.3 中显示的候选参考基因列表是经过特别挑选的,以选择属于不同功能类别的基因,从而减少基因可能共调的机会。一个明显的例外是 GAPDH,它有两个版本。虽然这并不影响本分析,但最佳做法是避免多个可能被怀疑共同调控的基因条目。
第一个要演示的算法是 geNorm。该算法通过计算称为 M 值的基因稳定性度量来评估基因的稳定性,而 M 值则基于所分析的候选参考基因与数据集中所有其他候选参考基因之间的成对比较。该过程以迭代的方式进行,也就是说,在本示例中,首先对所有 15 个候选参考基因执行该过程,剔除最不稳定的候选基因,然后对剩余的 14 个候选基因重复该过程,剔除第二个最不稳定的候选基因,依此类推,直到剩下两个参考基因为止。一种情况可能是所有候选参考基因都表现不佳。另一种情况可能是所有候选参考基因都表现良好。为了区分这两种情况,一个有用的准则是 M 值低于 0.5 的参考基因可被视为稳定表达。
要演示的第二种算法是 NormFinder,它是一个免费提供的参考基因分析软件包(附录 B,附加资源)。其基本算法采用类似方差分析的方法来评估参考基因的稳定性,即对整体和亚组进行变异分析。这样做的一个好处是,得到的测量结果与基因表达水平直接相关。因此,Cq 单位的标准偏差为 0.20 代表特定候选参考基因拷贝数表达水平约 15% 的变化。
为方便起见,本演示中使用 GenEx (MultiD) 数据分析软件访问这两个分析软件包,但它们也可以作为独立软件包提供(附录 B,附加资源)。
图 10.7 中显示的柱状图说明了使用这两种算法根据各自的稳定性指标对参考基因进行排序的情况。此外,显示NormFinder累积标准偏差的图表表明,最多三个最佳参考基因的组合可能会提高稳定性。
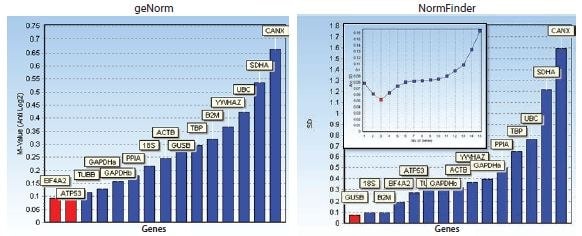
图 10.7.条形图显示稳定性指标:GeNorm 的 M 值和 NormFinder 的标准偏差。此外,NormFinder 的累积标准偏差图显示,最多可将三个最佳参考基因组合在一起,从而提高稳定性。该数据集是根据表 10.3 所示候选参考基因设计的检测方法生成的,并在两个不同处理组的人体细胞培养物上进行了测量。请注意,在这种情况下,参考基因稳定性算法 geNorm 和 NormFinder 在最佳参考基因的选择上并不一致。
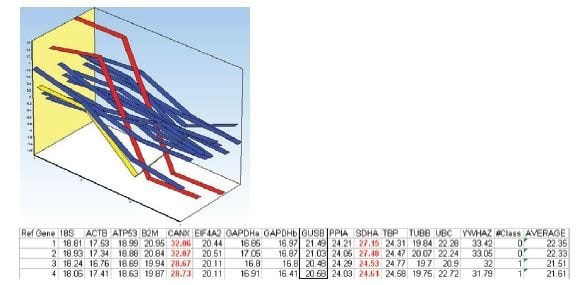
图 10.8.各治疗组两个样本候选参考基因的平均中心表达谱。样本 1 和 2 属于第一处理组,样本 3 和 4 属于第二处理组。SDHA 和 CANX 的表达谱用红色表示。UBC 的表达谱用黄色表示。表中列出了数据集中测得的 Cq 值。
由于表达谱存在偏差,SDHA和CANX可能受到不同治疗方案的调控,因此不适合作为参考基因。从数据集中移除这两个基因并重复分析后,两种算法的结果一致,参考基因的最佳选择是 EIF4A2 和 ATP53(图 10.9)。在 NormFinder 对累积标准偏差的计算中,增加更多的参考基因显然不会提高稳定性。
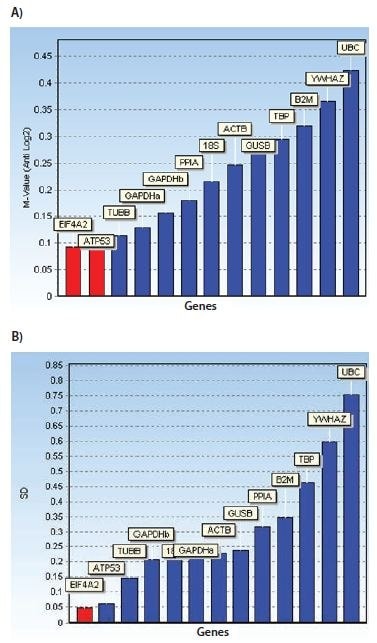
图 10.9.对表达谱和测得的 Cq 值(图 10.8)的检查引起了人们的关注,即 SDHA 和 CANX 可能在所应用的检测中共同调控。共同调控可能会破坏参考基因稳定性算法。条形图显示稳定性指标:A) geNorm 的 M 值,B) NormFinder 的标准偏差。数据集与图 10.8 中使用的数据集相同,只是删除了 SDHA 和 CANX 的数据。请注意,在缩小数据集的情况下,参考基因稳定性算法 geNorm 和 NormFinder 在最佳参考基因方面的结果是一致的。
本例中的数据分析说明,同时使用 geNorm 和 NormFinder 可以识别共调控的候选参考基因,并在进一步研究中剔除这些基因,最终识别出的参考基因比使用单一分析更有把握。鉴定和选择稳定的参考基因可提高数据分析的安全性。
可供选择的归一化方法
虽然参考基因归一化是检测归一化的最常用方法,但在某些情况下这种方法并不适用,例如需要比较异质样本组中的大量基因,或分析 miRNA 时。
根据组织质量或细胞数归一化
测量细胞数或组织质量作为归一化因子并不像最初看起来那么简单。细胞培养实验相对容易根据细胞数进行归一化。但是,添加某种处理方法可能会影响细胞形态,从而使细胞数量与表达的总 RNA/基因之比(与对照培养物相比)变得复杂。
生物组织在受试者体内和受试者之间可能存在高度异质性,当健康组织与患病组织进行比较时,差异会更明显。
即使是表面上不太复杂的组织(如血液),其细胞数量和组成也会有很大差异,因此表面上健康的供体之间的基因表达也会有很大不同18。
用于纯化核酸的过程中的任何延迟都会导致所测得的 RNA 发生变化。例如,处理外周血单核细胞和从细胞中提取 RNA 的延迟会导致基因表达发生相当大的变化19。提取程序的基本方法也是技术差异的主要来源。即使是血液衍生细胞采样和 RNA 纯化所选择的分离过程也会导致表观基因表达谱的差异20。因此,标准化的首要考虑因素是确保所有样本的采集和处理过程完全相同。然后,关键是要进行充分的质量控制,以确定样本的浓度、完整性和纯度(Sample Purification and Quality Assessment and associated protocols in 附录 A).
归一化到 RNA 浓度
至少,模板浓度(用于 qPCR 的 DNA 或用于 RT-qPCR 的 RNA)的估算是重要的,正如在
对全局基因表达进行归一化
在测量大量靶标时,分析人员可以估计全局基因表达的平均值,并识别偏离该平均值的受调控 RNA 序列。这种方法通常用于基因表达阵列的归一化。
最近探索的另一种方法是测量存在于许多 mRNA 中的内源性表达重复元件 (ERE)。许多物种都含有这些重复元素(灵长类动物的 ALU、小鼠的 B 元素),它们可以提供 mRNA 部分的估计值。对这些目标序列的测量已被证明可作为传统的归一化系统9 (Le Bert 等人,正在准备中),并可为复杂的实验提供通用的解决方案或替代方案,因为在这些实验中无法获得稳定的参考基因组合。
miRNA数据的归一化
目前还没有关于 miRNA 通用参考基因的报道。因此,归一化系统的选择仍然是经验性的。在可能的情况下,可从全基因组方法(即微阵列)中确定稳定不变的 miRNA。小核仁 RNA(snoRNA)也被用作参考基因。当稳定的参考基因未知,而几百个靶标已被分析21,22,23时,全基因表达也是对 miRNA 表达进行归一化的有用方法。这种方法更适用于那些采用 cDNA 多路复用形式捕获所有 miRNA 的方法,如 Exiqon 和 miQPC、
生物和技术复制品
归一化的目的是避免系统误差,减少最终统计分析的数据变异性。为统计分析设置数据的另一个重要方面是使用数据重复。
生物重复对于统计分析是绝对必要的。统计显著性水平通常设定为 5%。对于接近这一显著性水平的生物效应,可能需要至少 20 个生物重复来确定测定的显著性水平(1:20 相当于 5%)。事实上,有人认为要准确估计显著性25,至少需要记录 50 倍数量的观察结果,即大约一千个生物样本。当然,由于实际条件的限制,很少有机会进行这种水平的生物重复。此外,准确估计达到特定显著性水平所需的生物重复样本数量还取决于数据的可变性水平。尽管如此,重要的是要认识到,低估得出可靠结论所需的生物重复次数是一个常见错误。建议进行初步的试验研究,评估测定的固有变异性和可观察到的生物效应的潜在规模,以便为估计必要的生物重复次数26打下良好基础。相反,技术重复用于备份样本(以防某些样本在技术处理过程中丢失)和改进数据准确性评估。如果假设成立,即在技术处理过程的每个阶段,技术复制品都围绕准确测量值随机变化,则技术复制品可以提高数据的准确性。技术样本的平均值更接近准确测量值。通过注意具有预定变异性(即标准偏差设为 1)的模拟数据集中置信区间的大小,可以说明平均技术样本的效果。如表 10.4 所示,置信区间随着技术重复(样本)数量的增加而变小,这表明对精确测量的估计更加精确。此外,在技术重复次数较少的情况下,置信区间的缩小最为显著。重复次数从 2-3 次增加,置信区间从 8.99-2.48 减小,即精确测量估计值的精度提高了 3 倍多。虽然增加重复次数会继续提高测量精确度的估计值,但其影响程度是递减的。因此,在技术处理变异性是一个问题的情况下,使用三重样本而不是重复样本显然会有很大的优势。
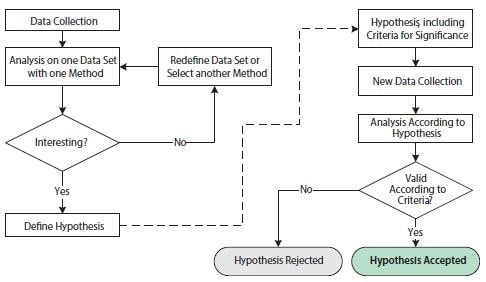
图 10.10.探索性和确认性统计分析操作流程图。图中虚线箭头之前的左侧显示的是探索性统计研究中的操作。图中虚线箭头后的右侧显示的是确认性统计研究中的操作。
探索性研究的目的是用一种或几种不同的技术分析数据,以证实一个假设。为了支持一个或多个假设,可以重新定义数据集和/或反复使用不同的分析技术。因此,探索性研究对任何科学问题的具体情况都非常灵活。不过,对一个数据集进行假设检验的反复探究可能会导致一些问题,从而破坏统计结论。这是因为多重检验的缘故,多重检验指的是一个统计检验如果有几个独立的假设,则更有可能得出正向的显著性结果,而且这种可能性会随着检验更多的假设而增加,即使基本的概率分布是相同的。
确证研究的要求基于更为严格的统计标准。首先,研究假设,包括显著性标准,需要在收集数据和分析之前确定。此外,用于分析的数据集必须是专门为此目的收集的。在确认性研究中重复使用探索性研究的数据集在统计学上是不正确的,因为该数据集本质上有利于提出的假设。
统计测试
对于统计测试,要分析观察到的现象是随机发生的可能性。这被称为零假设28。如果根据零假设,观察到的现象是罕见的,那么结论就是零假设不可能成立。零假设被拒绝,而替代假设的显著可能性被接受。
观察到的现象因随机机会而发生的估计可能性称为 p值。 p值的测量范围为 0 到 1,或等同于百分比单位。确证研究的统计标准包括一个α临界值,在此临界值下计算出的 p值表明观察到的现象具有显著性。通常使用的α截止值为 5%,但必须根据研究对象的具体情况进行调整,以符合所需的必要标准。
目前已开发出许多算法,用于在各种假设条件下和出于不同目的计算 p值。一种常见的算法是学生 t 检验。学生 t 检验用于根据两组数据平均值的差异计算 p值。学生 t 检验的主要假设是两组数据是独立的,且符合正态分布。与非参数统计检验29相比,学生 t 检验的一个优点是功能强大。与学生 t 检验等效的非参数检验可能是最著名的非参数统计检验之一:Wilcoxon 秩和检验(有时称为 Mann-Whitney U 检验;不要与用于比较两个配对组的 Wilcoxon 符号秩检验混淆)。与参数统计检验(如学生 t 检验)相比,非参数统计检验(如 Wilcoxon 秩和检验)的优势在于它们不依赖于数据集分布的先验假设。可以使用 Kolmogorov- Smirnov 的正态分布检验来决定是使用 Student's t-test 还是使用其中的一种非参数检验
除了选择算法进行&.nbsp;p值计算算法的选择外,还可以对输入到 p值计算算法中的数据集进行处理,以便于观察数据集中所需的属性。原始数据操作步骤与 p值计算算法的选择相结合是构建假设模型的一部分。
在统计分析的探索阶段,构建假设模型的自由度很高,这也是科学探索的一个重要部分。但是,使用科学的统计方法永远无法证明假设。正确的科学方法是提出一个零假设,使用一个独立的(最好是新收集的)数据集,并根据确证研究流程图(图 10.10)接受或拒绝零假设。
单变量分析的可视化技术
正如有许多分析方法可供选择一样,也有许多数据可视化技术可供选择。对于单变量数据分析,简单的条形图和相关的误差条是一种合适的可视化技术。尽管这是一种常见且简单的可视化技术,但仍有一些问题值得强调。首先,误差条可以说明不同的变异性来源;数据的固有变异性(标准差,SD)或确定平均值的精度。其次,确定平均值的精度可以用不同的方法来说明,但最终取决于数据的固有变异性与样本数 (N) 的组合,其原始形式称为平均值的标准误差 (SEM, 公式 1):
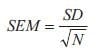
公式 1.SEM
然而,SEM 并不是一种非常直观的测量方法,而且以一种有意义的方式比较不同实验的 SEM 并不简单。一种更常用的方法是置信区间 (CI, 公式 2),它能以图形方式说明估计平均值的精度并显示统计显著性:
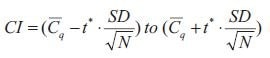
公式 10-2.Cl
从置信区间公式中可以看出,SEM 是标准差 (SD) 与样本数 (N) 平方根的比值,因此置信区间显然是以 SEM 为基础的。置信区间的下限是用平均值减去 SEM 乘以 t 分布的百分位数得出的。置信区间的上限是由 SEM 乘以 t 分布的一个百分位数与平均值相加得出的。置信区间的置信水平由与临界值 t* 相关的置信水平设定;通常为 95% 的置信水平。
图 10.11 显示了一个条形图,其中的误差条表示每个实验组内 95% 的置信区间,突出显示了在使用多种药物剂量治疗后,不同器官样本中基因表达的平均估计值的不确定性。此外,对照样本与来自不同药物剂量反应的三个不同样本中的每个样本之间的基因表达差异的 t 检验统计显著性 p值用星号符号表示。按照惯例,一个星号对应低于 0.05 的 p值,两个星号对应低于 0.01 的 p值,三个星号对应低于 0.001 的 p值。
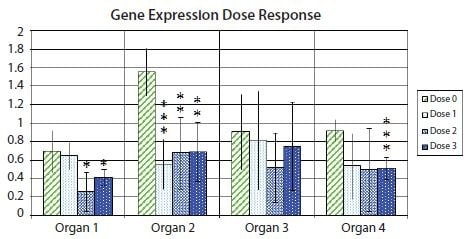
图 10.11.相对于每种器官类型中表达量最低的样本,相关基因相对于一对参考基因表达量的折合变化(log2)。柱高表示未处理(剂量 0)样本或以三种不同药物剂量(剂量 1、剂量 2 和剂量 3)之一处理的样本组中多个样本中该基因的平均表达量。误差条表示平均表达量的 95% 置信区间估计值。一个星号表示与未处理样本组的平均值相比,处理样本组的平均值在统计学上有 5%的显著差异;两个星号表示在统计学上有 1%的显著差异;三个星号表示在统计学上有 0.1%的显著差异。
鉴于星号符号隐藏了 p 的绝对值,因此通常鼓励在表格中列出 p 的绝对值,如 Table 10.5 中的示例所示。8125rem;">p ,如 表 10.5 中的示例所示。这背后的一个原因是,例如 0.032 的 p 值只比 0.055 的 p 值稍微 "显著 "一些。在决定将数据归类为显著性时,准确地使用哪个临界值时,像这样的边缘情况可能会导致一些困惑。在实际情况中,0.051 的 p 值可能与 0.055 的 p 值同样重要。8125rem;">p值为 0.049,但严格的(尽管从根本上说是任意的)0.05 临界值会将一个归为显著,而另一个归为不显著。
不过,条形图可视化还有一种变体,它利用均值差的置信区间来避免传统条形图的许多(如果不是全部)缺点24。利用均值差的置信区间,可以直接估计统计显著性和相关误差条,同时突出生物效应大小和数据变异性 图 10.12 显示了 图 10.11中使用的数据的均值差置信区间变体。请注意,不包含均值间零差的置信区间对应于与 p值截断点( 图 10.11 和 表 10.5中为 5%)相对应的置信水平上的显著结果。
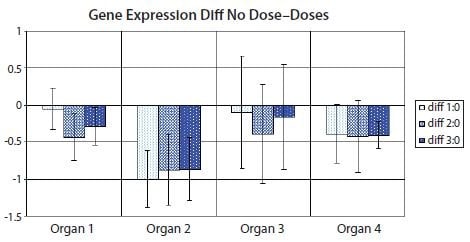
图 10.12.条形图显示了图 10.11 数据集中未处理样本组(剂量 0)与处理样本组(剂量 1、剂量 2 或剂量 3)的平均值之间的差异。误差条显示平均值差异的置信区间。不与 x 轴交叉的误差条表示相应的均值比较在 t 检验中具有 5%的统计学意义。聚合酶链反应技术,当前的创新-第 3 版,泰勒与弗朗西斯集团有限责任公司出版。经 Taylor and Francis Group LLC Books 许可,通过版权清除中心以图书/电子图书格式转载。
多变量数据是针对每个采样单元的多个变量收集的数据。 图 10.11 和10.12 中使用的数据是多变量数据,因为它们取决于剂量和器官类型等变量。然而, 图 10.11 和 10.12 中的统计分析仍然是单变量的,因为每个表示(条形图)只说明了一个变量(基因表达)相对于其他变量的固定测量值。对于多变量数据分析技术,分层聚类和主成分分析是数据表示的良好选择。
分层聚类
表征数据最简单有用的方法之一是在散点图中绘制数据(例如,绘制测量的 Cq&Cq&Cq&Cq&Cq)。sub>q 值)。一维或二维图便于人眼观察。使用适当的工具也可以绘制三维图,但更高维度的图很难可视化。不过,对于探索性研究来说,数据集本身就是多维的,因此整个数据集的散点图可能会变得不切实际。
对探索性研究数据进行特征描述和可视化的另一种常用方法是分析散点图中数据点之间的距离度量。目前存在不同的距离测量方法,包括欧氏、曼哈顿和皮尔逊相关性。随着计算能力的提高,即使是维度远高于三维的多维数据,也可以直接计算距离。对于聚类分层聚类,需要执行以下迭代过程:1) 找到两个最接近的对象并将其合并为一个聚类;2) 通过聚类方法将新聚类定义为一个新对象;3) 重复 1) 直到所有对象都合并为聚类30。可供选择的聚类方法包括沃德法、单链法和平均链法31。
对 qPCR 数据的分层聚类树枝图的解释通常会得出基因表达谱相似性的结论。在探索性研究中,这些相似性可用于提出有关基因表达核心调控的假设,这些假设可在随后的确证研究中被接受或否定。分层聚类树状图的优点包括可视化相似性关系的清晰度。另一方面,由于相似的表达谱可能是假设中多余的属性,因此在提出假设时,对相似性测量的强调可能会被认为是一种限制。为了回答所需的假设,识别以特定组合形式相互补充的表达谱集可能具有更高的价值。
主成分分析
对探索性研究的数据进行特征描述和可视化的另一种流行的替代方法是利用整个多维数据集中包含的信息,选择所需的属性并将其投射到低维散点图上,如二维或三维图。这可以通过主成分分析(PCA)32,33,34,35来实现。在这里,数据集(即 qPCR 测量的表达谱)的原始坐标系被转换到一个新的多维空间,在该空间中构建了新的变量(主成分:PC 或因子)。每个 PC 都是原始数据集中各研究对象的线性组合。根据数学定义,PC 是按照重要性的先后顺序提取的。这意味着第一个 PC 解释了数据中的大部分信息(方差),第二个 PC 解释的信息较少,以此类推。因此,前两个或三个 PC 坐标(称为分数)可用于将整个数据集投影到一个方便的小维度上,适合在二维或三维图中进行可视化。通过使用前两个或三个 PC 进行表示,可以得到反映数据集中最大变异性的投影。来自实验设计条件的变异预计是系统性的,而混杂变异预计是随机的,因此在适当的条件下可能需要这种表示方法。
正如之前提到的分层聚类,对 qPCR PCA 的解释往往会得出基因表达谱相似性的结论。虽然 PCA 和分层聚类可对基因表达共调模式产生互补的见解,但这两种技术都侧重于基因表达谱的相似性。这就限制了在探索性研究中仅使用这些技术就能发现的假设类型。为了扩大探索性研究中生成假设的范围,最近提出了一种假设驱动的多元分析方法24。假设驱动、定制设计的算法可以识别与生物相关的假设,否则常用的多元数据分析技术可能会遗漏这些假设。
材料
如要继续阅读,请登录或创建帐户。
暂无帐户?